最近在看量化多因子基础方面的资料,直接从实操层面入手比较难理解量化的思维方式,本文整理了经典资产定价模型,帮助理解金融量化分析以及多因子的发展。
均值-方差模型
Harry M.Markowitz 于1952年发表了《portfolio Selection》一文,其中提出了均值-方差模型。第一次使用数理分析定量的证明了投资中收益与风险的关系,也成为了现代金融定量分析的开端,为后来的现代投资组合理论(MPT)奠定了基础。
均值-方差模型中最重要的一个概念就是用均值和方差来描述收益与风险。均值指的是投资组合的期望收益率,也就是组合中每个资产的收益率的加权平均,这里的权重是资产占组合的比例。
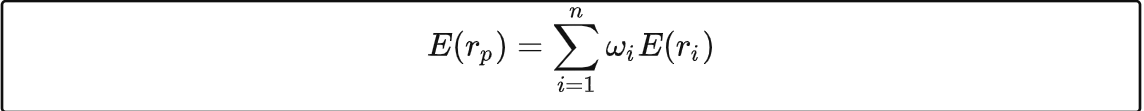
这里E()是期望符号,量化中的收益率大部分都是使用期望的概念。E(rp)是资产组合p的期望收益率,wiE(ri)是资产i的期望收益率 * 资产i在组合中的权重,整个组合的收益就是每部分收益的加权累加∑。
方差指的是投资组合的风险性(收益的波动性)。方差的公式中涉及到了协方差Cov()的概念,协方差可以理解为衡量两种资产的收益率变动的相关程度。
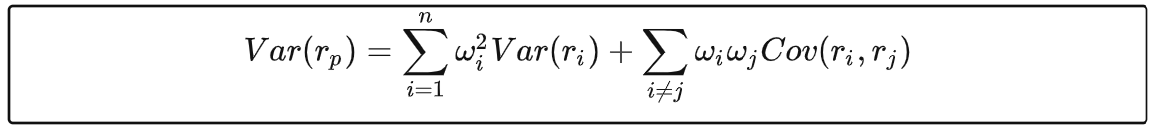
Var(rp)是资产组合p的方差,wi和wj分别是资产i与j的权重,Var(ri)是资产i收益的方差,Cov(ri, rj)是资产i与j收益的协方差。
正是因为方差公式中包含了协方差的部分,大家发现了资产组合的风险并不是每个资产风险的加权平均,而是可以通过资产间的相关性进行调整和对冲。
当知道了风险和收益的求解方式后,接下来的问题便是给定期望收益,给定组合内的资产,那怎么样的资产权重才能达到风险最小?
Markowitz告诉我们这个就是求解给定组合期望收益下,如何使组合方差最小?求解出来的图形的上半段便是大名鼎鼎的有效前沿(efficient frontie)。有效前沿上的点便是当前收益率下,风险最小的组合配置。
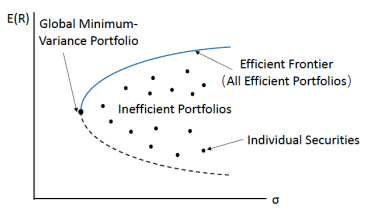
如果组合中加入无风险资产,那么原本的有效前沿就不再有效,通过从无风险收益率Rf对马科维茨有效前沿做切线,就可以得到资本市场线(CML)用来表示新的最优资产组合集。CML的斜率就是现在常用来衡量波动性的夏普率(sharp ratio)。

均值方差模型无法在真实环境中使用的最大原因是需要有市场中所有风险资产或者可投资风险资产的预期收益率和预期协方差矩阵,而现实情况都是使用历史数据来计算预期收益率与预期协方差,这个就回到了最初的问题,真实世界的市场是随机的,历史无法代表未来。
CAPM 模型
在均值-方差模型提出后,一众经济学家以实证角度出发,对最初的模型进行了简化,Sharp 提出了资本资产定价模型(CAPM)。CAPM 的理论是建立在投资者都使用 Markowitz 的理论进行资产组合投资的情况下,形成的市场均衡状态(供需完全相等,即价格完全反应价值),这个时候可以使用一个线性关系式来描述资产预期收益与风险的关系,认为一个资产的预期收益率与衡量该资产风险的一个尺度β值之间存在正相关关系。这个模型也成为了现在金融学的理论基础。
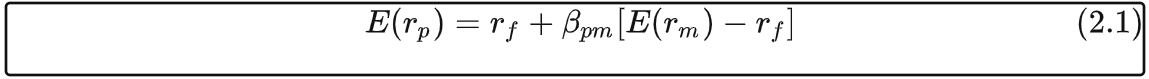
E(rp)代表投资组合的预期收益率,rf为无风险收益率,βpm是市场m的风险暴露系数,E(rm) - rf 是市场的超额收益。

β可以看作某个资产或者资产组合的超额收益率(减去无风险收益后的收益率)对于其所在市场超额收益率的敏感度。这个贝塔可以用资产和市场的协方差/市场的方差计算,可以看出来其实是在度量资产和市场的相关性相对于市场波动性的程度,也被成为因子载荷。而市场的超额收益部分后来被称作了市场因子,为之后蓬勃发展的因子流派打下了理论基础。
之前说过 CAPM 是建立在 Markowitz 资产组合理论的前提下,而且还有很多附加的假设:
1、投资者对资产的评价标准仅从期望收益和风险两方面考虑;
2、投资者在其他情况相同下,总是希望可以获得更多的收益,投资者总是不满足的;
3、投资者是风险厌恶的,在预期收益率相同的情况下,投资者会选择风险较小的那个组合;
4、投资者可以在市场上以相同的无风险利率进行无限制的借贷;
5、投资者对资产的持有保持相应的一段时期,并且所有投资者的时期视野都是相同的;
6、投资者对信息的处理结果是一致的,大家都具有相同的预期;
7、没有市场交易成本;
8、投资者可以根据自己的需要买卖任意数量的证券;
9、信息是免费的并具有完全流动性;
随着对这个模型研究的越多,大家发现单独的市场因子并不能解释很多真实市场中的金融异象(资产实际收益偏离模型预期收益),于是诞生了之后的多因子模型。
ICAPM 模型
ICAPM 是对 CAPM 的一种补充,用来补充 CAPM 中市场因子无法解释的部分。ICAPM 提出投资者在做决策时不止考虑当时投资组合的情况,还要考虑未来会对投资组合产生影响的风险因素,这些风险因素被称为状态变量,在公式上表现为CAPM模型上再加上由多个状态变量产生的风险溢价。
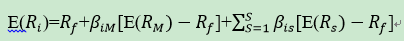
公式前半部分与CAPM相同,后半部分βis表示资产i在状态s上的因子暴露,[E(Rs)-Rf]是状态s的超额收益,然后就是所有状态s的累加∑。
ICAPM 模型在理论上比静态的 CAPM 包含更多的解释因素,但是实际计算和分析难度很大,状态的选取与因子暴露β的计算都是脱离真实市场的,所以并没有实际的运用指导,但是却为后来的 Fama-French 三因子模型奠定了基础。Fama通过解释 ICAPM 中的状态变量为多因子组合,在完全沿用 CAPM 模型的分析下将分析思路从状态变量转换到多因子分析模型,为多因子研究奠定了基础。
APT 模型
APT 模型的的出现源于 Stephen Ross 教授对 CAPM 模型过于严苛假设的批判,转而从均衡市场的完全套利角度出发提出了套利定价理论。APT 认为资产的收益率由多个资产间普遍性的风险因素以及该风险的暴露程度决定,不同的资产在这些普遍性风险因素上的风险暴露程度不同,导致了资产间收益的不同。换言之如果两个不同的资产在这些普遍风险因素上的风险暴露都是相同的,则两个资产应该有相同的预期收益率,否则就会出现套利机会,市场也会被套利行为拉回均衡状态。
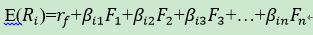
E(ri)代表资产i的预期收益率,rf为无风险收益率,βin表示资产i在风险因素n上的暴露程度,Fn表示第n个普遍性的风险因素。
APT 比 CAPM需要的假设少,主要是下面三条:
- 投资者有相同的预期
- 投资者规避风险同时追求收益最大化
- 市场是完全流动且信息透明
APT 完全不依赖 Markowitz 的投资组合理论,而且提出了多个资产普遍性风险这个概念,也就是后来多因子的概念。虽然理论的出发点是市场套利,但是公式形式上已经十分趋近多因子模型。不过 APT 没有对因子的定性给出经济学上的解释,也没有阐述该用什么因子和用多少个因子。
Fama-French 三因子模型
20世纪70年代以来,学术界逐渐发现某种风格的一类股票有较大概率能够战胜市场。Basu 发现了盈利市值比效应(EP),Banz 发现了小市值效应,账面市值比(BM)和债务市值(DM)效应也被发现。于是 Fama 和 French 利用APT的多因子思路,开始在 ICAPM 模型的基础上寻找其它可以解释异象的因子,最终提出了规模因子(SMB)以及价值因子(HML)。
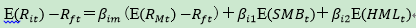
E(Rit)-Rft为t时期资产i的超额收益,βim是资产i在市场因子下的因子暴露, E(Rmt)-Rft是t时期市场组合的超额收益,βi1是资产i在规模因子下的因子暴露,E(SMBt)是规模因子在t时期的收益率,βi2是资产i在价值因子下的因子暴露,E(HMLt)是价值因子在t时期的收益率。
Fama-French取市值作为规模因子,市值账面比作为价值因子,这两个因子与收益率的协方差不为0,有着无法通过分散化而消除的系统性风险,且这些风险独立于市场因子的系统性风险存在。SMB(small minus big,小减大)是一组小市值股票组合与一组大市值股票组合收益率的差值,用来描述不同的股票收益率中表现出来的与总市值相关的变动。 HML(high minus low,高减低)是一组高账面市值比股票组合与一组低账面市值比股票组合收益率的差值,用来描述不同的股票收益率中与账面市值比相关的变动。三因子模型解释了很多之前 CAPM 单因子模型无法解释的异象。
从三因子模型中我们可以看出,量化因子分析的不是资产在时序上收益的变动,而是某一时间截面下,资产间预期收益的差异原因。因子可以被理解为APT中提出的普遍性的风险,也就是构成最终收益的某种成分。Fama-French 三因子模型在出现一段时间后,学界又陆续发现了一些独立于市值与市值账面比的因子,这也正式拉开了多因子研究的序幕。
Fama-French 五因子模型
随着多因子研究的逐渐深入,Fama 和 French 随后针对三因子模型存在的异象进行了深入研究。他们发现股票收益率与股票的盈利能力与投资增速间存在显著关系,且这种关系不属于市值与账面市值比可以解释的,随后Fama-French 认为盈利能力与投资增速可以通过股利贴现模型进行解释,于是在三因子的基础上增加了盈利因子(RMW)与投资增速因子(CMA)。
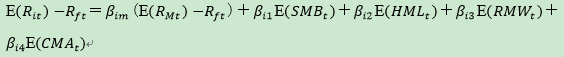
在三因子模型基础上添加了两个因子,βi3是资产i在盈利能力因子下的因子暴露,E(RMWt)是t时期盈利因子的收益,βi4是资产i在投资增速因子下的因子暴露,E(CMAt)是t时期投资增速因子的收益。
RMW(robust minus weak,强减弱)是一组强盈利能力组合与一个分散化的弱盈利能力组合收益率的差值,用来描述不同的股票收益率中与盈利能力相关的变动,其中盈利定义为t-1财年营业收入减去营业成本、利息费用、销售费用和管理费用后再除以t-1财年末的账面权益,Fama和French将这个变量称为“经营利润”。CMA(conservative minus aggressive,保守减激进,即资产增长低的减资产增长高的)是一组总资产增长率低的组合与一组总资产增长率高的组合收益率的差值,用来描述不同的股票收益率中与总资产增长率相关的变动,投资定义为t-1财年的新增总资产除以t-2 财年末的总资产。
五因子模型很好的解释了大部分三因子模型不能解释的异象,但是依然并不能解释所有收益率异象,在市场环境下,资产超额收益率对五个因子的因子暴露并没有完全捕获超额收益率的变化,说明依然还有没有被发掘的因子。资产定价模型从均值-方差发展到五因子,新模型基本都是构建在这些经典模型基础上,可以肯定的是资产定价是与时俱进的,没有永远的有效模型,只有无尽的探索。